Luftmodstand med CBL2

 

 

Forsøg med papirkageforme.

 

Formålet med øvelsen er at eftervise at der gælder:

a)  Papirkageformene  opnår  hurtigt en konstant fart

 

b)  Luftmodstanden har størrelsen                                          (*)

 

     hvor  k  er en konstant , A er papirkageformens tværsnitsareal, og v er størrelsen af

     faldhastigheden.

 

 

Apparatur: CBL2, ultralydssensor,   TI-83-plus , papirkageforme, vægt , målestok

 

Forsøget: Start med at indlæse Datamate-programmet i din TI-83-plus

Datamate skal sendes fra CBL-2 til ARC på TI-83-plus.

Forbind din lommeregner med CBL-2.  Tast 2nd link og vælg Recive på din TI-83 plus.

Tast Transfer på CBL-2 .  Programmet sendes nu fra CBL-2 til TI-83 plus.

Tast 2nd quit, når overførslen er forbi.  Tast  APPS for at finde programmet når du skal benytte det.

 

Vej  papirkageformene.

Mål diameteren på papirkageformene. ( På den brede del af kageformene, uden at

presse åbningen større).

Forbind ultralydssensoren med sonicindgangen på CBL2’en.

Forbind TI-83 med CBL2. (tryk godt ind).

 

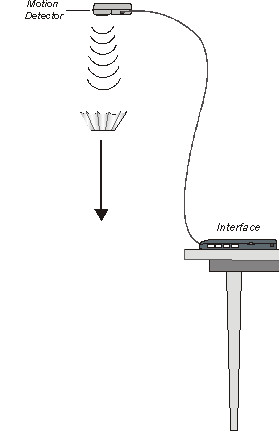
Hold kageformene ca 2 meter over jorden.  Direkte over ultralydssensoren ( På tegningen er sonden placeret over, resultatet bliver bedst hvis sensoren  ligger på gulvet, da bunden af kageformene er mere veldefinerede end de skrå kanter.)

 

 

 

 

 

 

 

 

 

 

 

 

Kør nu programmet Datamate.

 

Tænd lommeregneren og start DATAMATE programmet. Tast  for at resette programmet.

Vælg 1 SETUP, Vælg DIG, Vælg 1 MOTION (M) , Vælg MODE TIME-GRAPH, Vælg 2 TIME GRAPH , Vælg TIME Interval .05,  number of samples 100, tast 1 OK,
Tast 1 ok igen .

Nu begynder ultralydssensoren at klikke en lille lyd.

Vælg START for at begynde dataopsamlingen. Når ultralydssensoren bipper skal I slippe kageformene direkte over sensoren.  Sørg for at jeres arme og andet ikke kommer med , sensoren måler ud i en vifte.

Tast  for at se grafen over tid-strækning.

Hvis grafen ikke har en udsnit  med en ret linje, så kan det være fordi kageformen ikke har været over sensoren hele tiden, måske har i nogle gange målt afstanden til loftet.

Tast  og vælg 1 MAIN SCREEN.

Gentag dataopsamlingen hvis det er nødvendigt.

Farten af kageformene kan bestemmes ud fra hældningen på tid-strækning grafen.

 

Vi skal starte med at vælge region

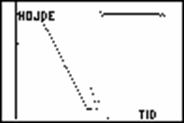
I starter med et billede som f.eks. dette:

 

 

I vælger nu ud:

 

 

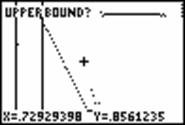
Og vinduer bliver herefter udsnittet:

 

 

På grafen bør der være et lineært udsnit, det er  det I skal klippe ud.

a.   Vælg 3 GRAPH fra main screen.

b.   Vælg sørg for at musen står ud for DIG-Distance , vælg 2 SELECT REGION.

c.    Placer  musen med  og  tasterne til det venstre endepunkt at det lineære udsnit og tast .

d.   Placer musen  ved det højre endepunkt af den lineære udsnit og tast .

e.   Se udsnittet ved at taste  . Der vil nu kun være det lineære udsnit på lommeregneren.

f.      Tast  og  Vælg 1 MAIN SCREEN for at vende tilbage til main screen.

 

I skal nu teste om målepunkterne er en lineær graf,

I givet fald er hældningen på linien lig kageformenes fart, og den skal bestemmes.

 

Vi skal nu finde den bedste rette linje.

a.   Vælg  4 ANALYZE fra main screen.

b.   Vælg 2 CURVE FIT fra ANALYZE OPTIONS.

c.    Vælg 4 LINEAR (DIST VS TIME) fra CURVE FIT skærmen.

d.   Noter hældningen i en tabel (A farten i  m/s).

e.   Tast  for at se den fittede linje sammen med data.

f.      Tast , og vælg 1 RETURN TO MAIN SCREEN.

 

     Overfør dine lister med TI-graflink til TI-Interactive .

     Tiden ligger i L1 , og afstanden ligger i L6.

 

Gentag forsøget med 2, 3, 4, 5, osv kageforme oven på hinanden og med forskellige størrelser kageforme,  så meget som tiden tillader.

Udfyld nedenstående skema  og  beregn kageformenes tværsnitsareal.

 

 

Store kageforme masse  M=                             , tværsnitsareal A=

 

antal n	regresionslinie	r	v  /(m/s)	v2 /(m/s)2
1
2
3
4
5
6

 

 

 

 

 

Små kageforme:   M=                             , tværsnitsareal A=

 

antal n	regresionslinie	r	v/(m/s)	v2/(m/s)2
1
2
3
4
5
6

 

 

Teori:

Hvis   v = konstant  Û     

 

Der gælder yderligere    

                       

                                               

 

 

 Idet n er antallet af kageforme og massen af n kageforme er          fås

             

                                                                                   

 

Tegn nu for hver af de to forsøgsserier en (n,v²) graf.     Giver det en ret linie?

Find  hældningen på den bedste rette linie , og bestem  herudfra for hver af de to forsøgsserier en værdi for konstanten k  (regn i SI-enheder).

Bliver k ens i de to forsøgsserier.

Kan man med rimelighed sige at formel (*) gælder.