Formål: At bestemme kapacitansen for to elektrolytkapacitorer,
samt at eftervise lovene for serie- og parallelforbindelse af kapacitorer.
Endvidere at se opladnings- og afladningskurver for kapacitorer.
Teori: En kapacitor kan lagre elektrisk energi og ladning.
En kapacitor kan oplades ved at blive forbundet i serie med en resistor og et batteri i et stykke tid.
For opladning af en kapacitor gælder at spændingen U over kapacitoren
med kapacitansen C, når den oplades gennem modstanden R, har følgende udtryk:
![]() , hvor U0
er spændingen til tiden 0.
, hvor U0
er spændingen til tiden 0.
For afladning af en kapacitor gælder at spændingen U over kapacitoren med kapacitansen C, når den aflades gennem modstanden R , har følgende
udtryk:
![]() .
.
Sidstnævnte er en eksponentiel aftagende funktion med halveringstiden
![]() ,
,
hvis man ud fra en graf har bestemt halveringstiden, og man har målt R, kan man altså beregne kapacitansen C.
Apparatur:
CBL samt TI-82 eller TI-83
Spændings- sonde
to elektrolytcapacitorer på 470m F
to elektrolytkapacitorer på 1000m F
en resistor på 100kW
9V batteri
ledninger og næb
Start med at downloade programmet CAPAC på din TI-82
Mål dernæst R med et W -meter.
Figur: 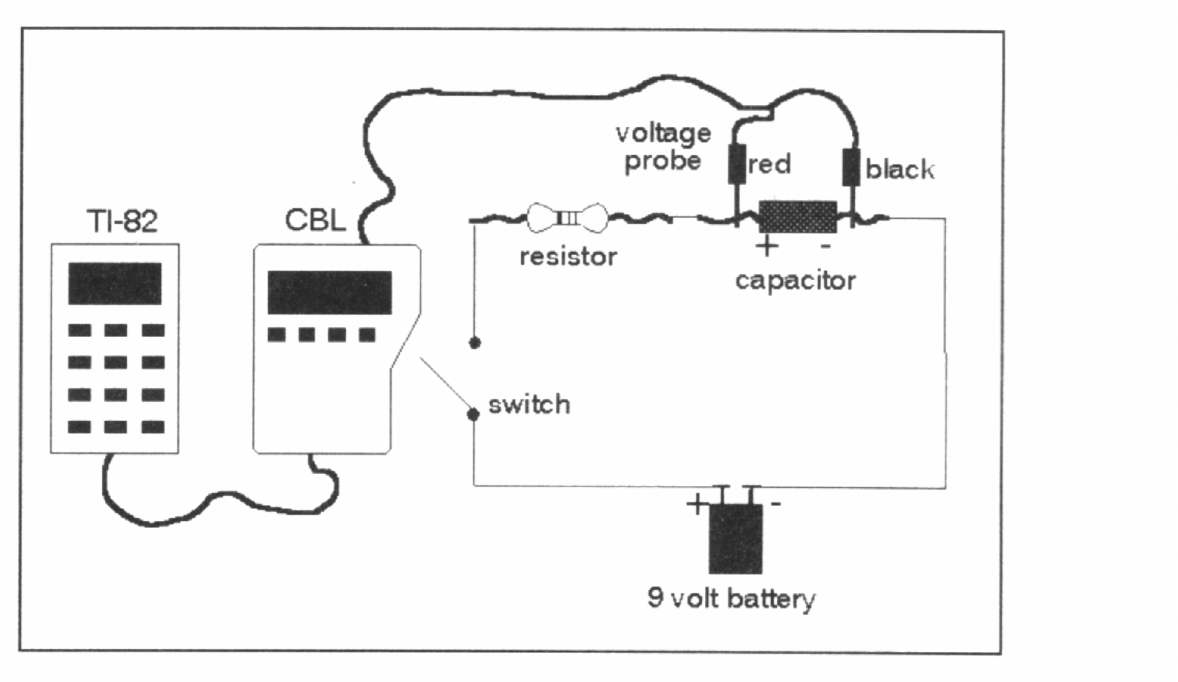
Forbind dernæst komponenterne som vist på figuren. Start med C=470m F
+ på kapacitoren er i den ende hvor den er bulet.
(enkelte har et sort mærke ved + polen).
Spændingssonden forbindes til CH1 på CBL’en.
Den røde pol skal forbindes til +.
Start nu CAPAC - programmet.
Vælg AUTO SCALA.
Vælg 1 , for en måling pr sekund.
Tryk ENTER mens du slutter kredsløbet.
Nu tegnes en opladningskurve.
Når den er tegnet kan du gemme den i din lommeregner eller få den tegnet ud ved hjælp af TI-graf-link i fysik .
Du skal ikke vente for længe, for kapacitoren kan godt miste lidt ladning ,
især hvis der ikke er meget tørt i lokalet.
Du skal nu køre programmet igen, men denne gang skal du fjerne batteriet og kortslutte ledningerne.
Nu tegnes en afladningskurve. Denne skal du også printe ud.
Du skal nu udføre en eksponentiel regression på dine måletal.
Du skal først indtaste tallene fra 1 til 99 i L(1).
Det gøres ved at skrive :
seq(x,x,1,99,1)® L1, seq findes ved LIST vælg 5.
Måletallene for spændingen findes i L4.
Du kan nu vælge EXPREG L1, L4.
Noter a,b,r og beregn halveringstiden og kapacitancen C1.
Sammenlign værdien med den påtrykte.
Fabrikanten siger at usikkerheden er 20 % passer det.
Den værdi I får vil altid være højere. De lover blot at den er mindst 470m F.
Vælg nu en ny kapacitor også med C=470m F.
Denne oplades nu hurtigt, idet I fjerner 100kW modstanden. Gentag forsøget med afladningen og noter a,b,r og beregn C2.
Sæt nu de to kapacitorer i en parallenforbindelse.
Gentag forsøget oplad hurtigt og tegn afladningskurven. Bestem a,b, r og beregn erstatningskapacitansen C12.
Sammenlign med den teoretiske værdi, der er beregnet ud fra de to første bestemmelser.
Gentag nu forsøget med en kapacitor på 1000m F.
Denne gang tager opladningen længere tid. Her skal I kun oplade hurtigt.
Under afladningen udføres igen eksponentiel regresion.
Vælg igen en ny kapacitor på 1000m F og gentag forsøget.
Sæt nu disse to kapacitorer i en serieforbindelse og bestem erstatningsresistansen.
Sammenlign med den teoretisk beregnede værdi.
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|