Eksempelbesvarelser - vektorregning i 3D

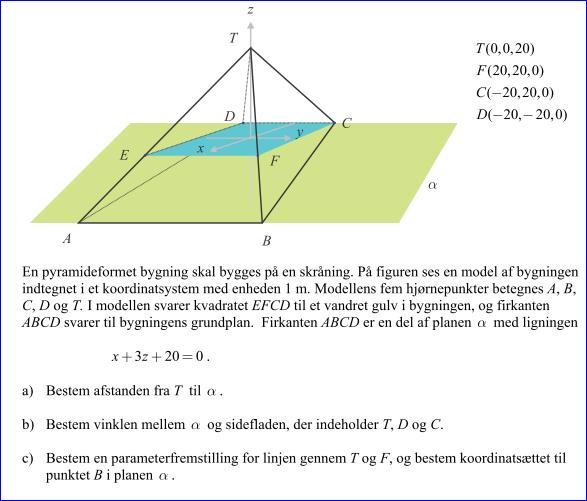
En eksempelbesvarelse

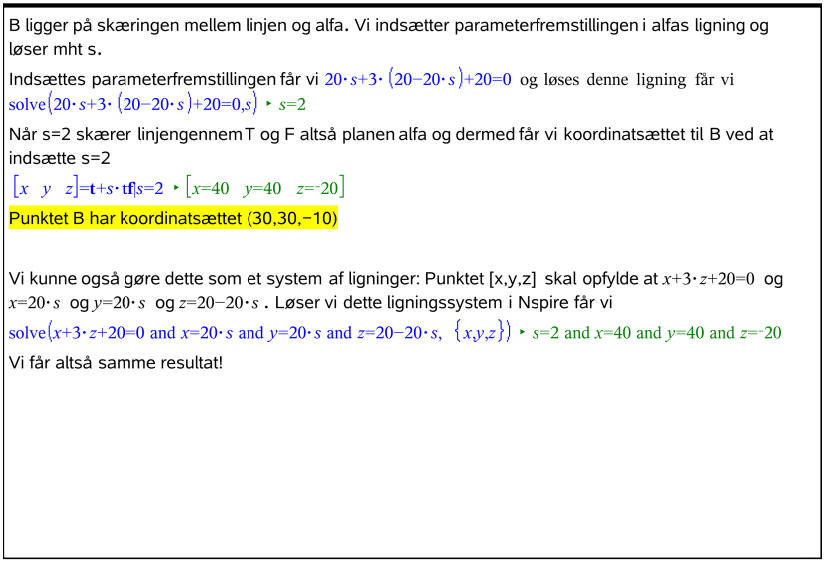
Kommentar til besvarelsen:

• Vektorregning er en udfordring for notationen. Man bør egentlig skrive vektorer med pile over, og det kan man også gøre i Nspire, men dels er det noget omstændigt og dels mister man den store regnemæssige fordel ved at kunne "regne med punkter". I besvarelsen ovenfor er løsningen at man i starten af opgaven skriver "I denne opgave vil jeg ikke skelne mellem punkter og stedvektorer. Jeg vil notere vektorer uden pile, men det vil fremgå af formuleringerne hvad der er vektorer." . Besvarelsen bliver ikke en skønhedsåbenbaring, men den vil give fuld point. Til gengæld skal man så huske at gøre opmærksom i teksten på hvornår man har med vektorer at gøre.

• Der er en uskreven regel om at tegninger altid er gode i geometriopgaver. I 3D-opgavaer giver det som regel ingen større mening. I denne opgave ville det ikke hjælpe meget.

• Standardnotationen om at punkter noteres vandret og vektorer noteres lodret er forladt fordi vi ikke skelner mellem punkter og vektorer. Hvis du blander lodret og vandret notation giver det mange problemer i Nspire.

• Når man regner vinklen mellem planer er der altid to svar der er lige gode. Hvis vinklen er 70grader så er den også 180-70=110grader.Hvis man regner vinkler mellem halvplaner som fx. to flader i en pyramide, så er det kun den ene af de to vinkler der skal findes. Et trick er at vælge normalvektorerne så den ene peger ind i pyramiden og den anden peger ud. Så er svaret rigtigt! Her kan vi betragte alfa som et plan der fortsætter, så her er det ligegyldigt. Svaret ovenfor er 63,43 grader, men 180-63,43=116,57 grader ville være lige så godt